Learning Network Games

Network games are a powerful tool for modelling strategic interactions between individuals or organisations played out on networks, where a player's payoff depends not only on their own actions but also on those of their neighbours. Such games have numerous applications in economics and social sciences, including studying the spread of influence in social networks, the dynamics of financial markets, and the formation of alliances in international relations. The study of network games typically assumes the underlying network structure to be known, which is often wishful thinking. Recently, machine learning approaches have been proposed to tackle this problem by leveraging the observed actions of players to learn the underlying network structure. In this blog post, we outline a novel approach that uses a transformer-like architecture to infer the network structure of a game without explicit knowledge of the utility function associated with the game.

Illustration based on based on Shutterstock.

This post is based on the paper Learning to infer the structure of network games, a collaboration with Federico Monti, Yan Leng, and Xiaowen Dong. The same blog post has been also published on Medium.

Network Games

Game theory is a mathematical framework for modelling and analysing situations where multiple decision makers interact with each other, and where the outcome of each decision depends on the actions of all players involved. In network gamesSee Games on Networks for an overview. the players are connected in a network (graph), and the outcome of the game depends not only on the players’ strategies but also on the structure of the network. Each player tries to maximise their utility function, which in the case of network games depends both on their own actions and the actions of their neighbours.

Equilibrium actions refer to a set of strategies where no player has an incentive to change their strategy, given the strategies of the other players. In other words, at equilibrium, each player’s strategy is optimal, given the strategies of the other players. In network games, the equilibrium actions depend on the graph structure, along with other parameters dependent on the game.

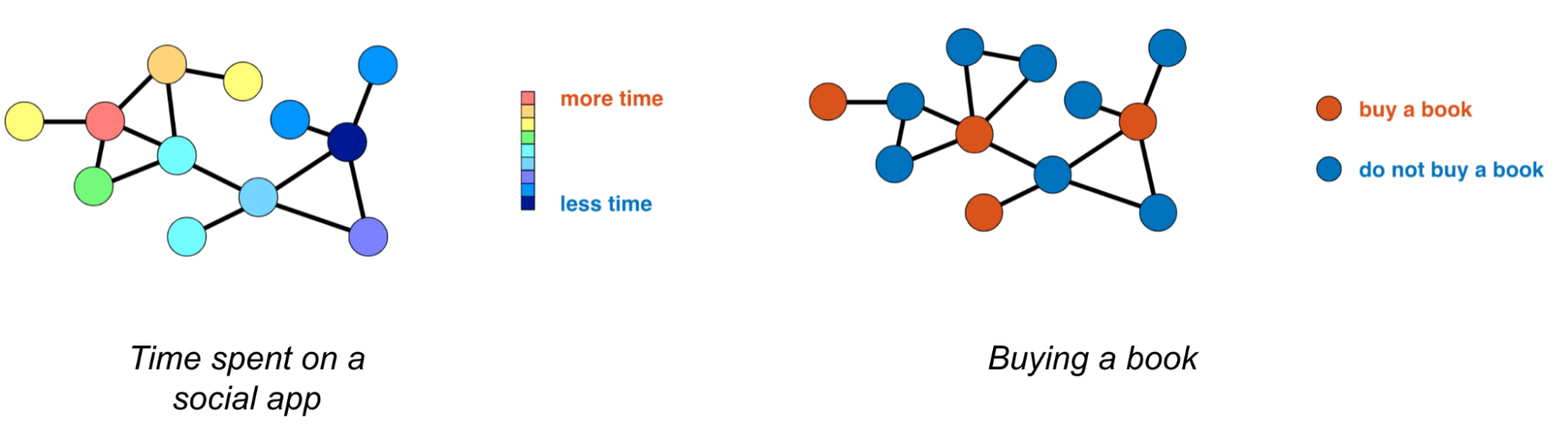
Consider, for example, a scenario where individuals on a social network can decide how much time to spend on the platform. In such a case, their behaviours may be influenced by their friends on the network, which creates a strategic interdependence between players. For instance, if Joe’s friends spend a lot of time on the platform, Joe might perceive a greater benefit from using the platform himself.

In a different setting, Joe is a user of an e-commerce platform deciding whether to buy a book. If his friend has already purchased the book, Joe might be less likely to buy it, as he can borrow it from his friend. These examples illustrate how actions in network games can be affected by the actions of neighbouring players, leading to strategic interdependence and the emergence of equilibrium actions.

Examples of network games. Left: a person is likely to spend more time on a social app if their friends are also spending time on the app. Right: a person has less incentive to buy a book if their friend bought it, because they can borrow it.

Inferring the Network from the Actions

In the above examples, we assumed to know the friends of Joe, i.e., the network structure of the game. However, in many situations, the underlying network structure is not directly available to us. Instead, we may only observe the equilibrium actions that result from the interactions between agents. In these cases, a crucial question is whether we can reconstruct the network structure based solely on these equilibrium actions. Knowing the network structure can be helpful in predicting behaviour and planning network-based interventions, such as marketing campaigns or information diffusion.

It was previously shown that, under specific assumptions about the mathematical form of the utility function and game types, it is possible to reconstruct the graph governing the network game. However, such assumptions can be unrealistic, especially when little is known about the game being played. To address this, in a recent paper we developed an approach that does not require assumptions about the form of the utility function and can be applied to a broad range of network games.

We start by studying three common types of network games, Linear Quadratic, Linear Influence, and Barik-Honorio. The three types of games differ by the form of the utility function, leading to different levels of smoothness of the actions in the graph.

Specific instances of three different types of games common in the game theory literature. The colours represent the actions taken by the players, which in this case are continuous values normalised between -1 and 1.

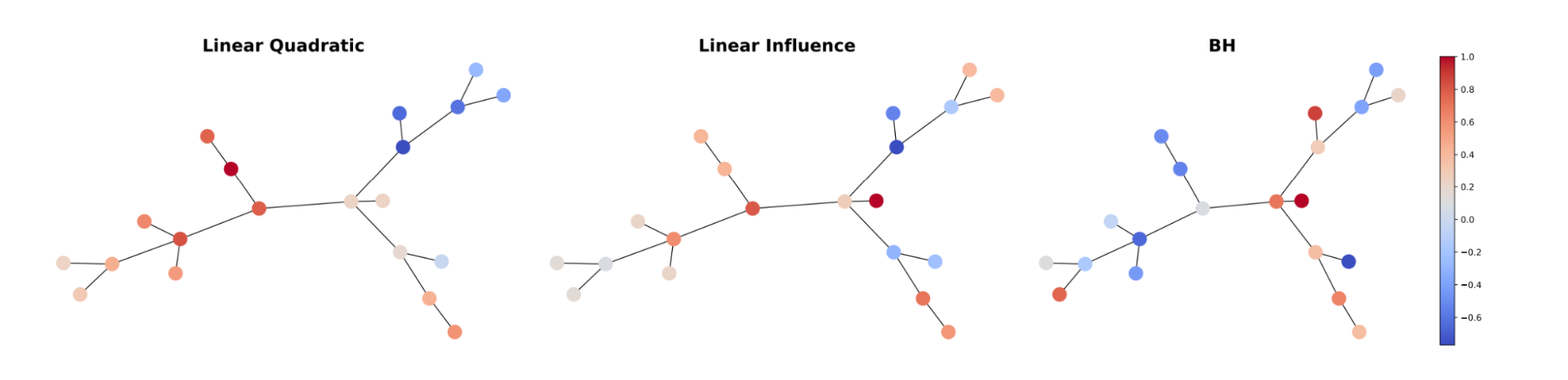
For example, Linear Quadratic games have the following utility function:

\[u_i = b_i x_i -\frac{1}{2} x_i^2 + \beta \sum_{j \in \mathcal{N}_i} a_{ij} x_i x_j\]

where \(x_i\) is the continuous action taken by player $i$, \(b_i\) is the player’s marginal benefit, \(\beta\) is a game parameter representing the strength of dependencies between actions of neighbours in the network, and \(a_{ij}\) is the entry in the adjacency matrix of the graph representing the strength of the connection between \(i\) and \(j\). The first term represents the marginal benefit for taking a larger action, the second (quadratic) term represents the cost for taking the action, while the third term represents the relation with the neighbours actionsIf $\beta$ is positive, the incentive of a player to take a higher action is increasing in the number of their neighbours also taking a higher action, something referred to as a strategic complement relationship. On the other hand, if $\beta$ is negative the incentive of a player to take a higher action is decreasing in the number of their neighbours taking a higher action (strategic substitute relationship).. Taking as example the aforementioned scenario of time spent on a social platform, the first term of the equation would capture the individual benefit from using the platform, such as staying up-to-date with the news, the second term would represent the cost from doing so, such as having less time to do other more important things, while the third term would capture the interdependence with the friends actions. In particular, \(\beta\) would be positive, as a person has an incentive to spend more time on the app if their friends (neighbours) do so.

The pure-strategy Nash equilibrium of Linear Quadratic games is:

\[\mathbf{x}^* = \big( \mathbf{I} - \beta \mathbf{A} \big)^{-1} \mathbf{b}\]

where \(\mathbf{x}\)* is a vector of dimension \(n\) (equal to the number of players, or nodes of the graph), \(\mathbf{A}\) is the unknown \(n \times n\) adjacency matrix of the graph, \(\mathbf{b}\) is the \(n\)-dimensional vector of marginal benefits of the players.

Similar formulas can be derived for Linear Influence and Barik-Honorio games. A formula for the equilibrium actions \(\mathbf{x}^*\) that generalizes all three games has the formIn this formula, the choice $f(\mathbf{A})=(\mathbf{I} - \beta\mathbf{A})^{-1}$ and $h(\mathbf{b})=\mathbf{b}$ yields a Linear Quadratic game, $f(\mathbf{A})=\mathbf{A}^{-1}$ and $h(\mathbf{b})=\mathbf{b}$ a Linear Influence game, and $f(\mathbf{A})=\mathbf{u}_1$ (the largest eigenvector of $\mathbf{A}$) and $h(\mathbf{b})=1$ a game of the Barik-Honorio type.

\[\mathbf{x}^* = \mathcal{F} (\mathbf{A}) \mathcal{H} (\mathbf{b})\]

where the function \(\mathcal{F} (\mathbf{A})\) accounts for the influence from the actions of one’s neighbours in the network and encodes the specific utility function of the game, and conversely, \(\mathcal{H} (\mathbf{b})\) is only affected by one’s characteristics, such as the marginal benefit of an individual player.

In the paper we further showSection 3.3 in our paper. that the players’ actions contain information about the spectrum of the graph, confirming that it is possible to reconstruct the graph structure from only the actions and justifying our approach outlined below.

Machine Learning Approach

To tackle the problem of inferring the network structure of a game, we approach it as a machine learning problem. We train a model to map the players’ actions to the network structure of the game, without any prior knowledge of the underlying utility function. To achieve this, we gather a dataset of actions and network pairs (\(\mathbf{x}\), \(\mathbf{A}\)) from games played with the same utility function (although this function is unknown to us). This allows us to avoid making strong assumptions about the utility function and instead train a model that is agnostic to it.

Such an approach is particularly useful in scenarios where social network and decision data exist for a small population, and we aim to learn the mapping from decisions to the network structure of a larger population. For instance, governments, public agencies, and researchers can collect social network data on a small population by asking individuals to nominate their friends, and then use the proposed method to learn the network interactions for a larger population in a cost-effective manner.

Our ML model has an encoder-decoder architecture that is invariant to the permutation of both the players and the games, corresponding to the rows and columns of the \(n \times K\) matrix \(\mathbf{x}\), where \(k\) denotes the number of games. To achieve this, we modify a Transformer model, which is naturally permutation-invariant over the set of nodes but not over the set of games.

Diagram representing the encoder-decoder architecture of our model. The $n \times K$ input matrix $\mathbf{x}$ containing the players’ actions is encoded into the $n \times F \times K$ tensor $\mathbf{Z}$, where $\mathbf{z}_{ik}$ is the embedding for node $i$ in game $k$, obtained by attending over the actions of the other players in the same game. $\mathbf{Z}$ is then decoded into the $n \times n$ adjacency matrix $\tilde{\mathbf{A}}$ where the entry $\tilde{\mathbf{a}}_{ij}$ contains the probability of an edge between $i$ and $j$.

Our encoder produces \(K\) vectors for each player as follows:

The scalar action \(\mathbf{x}_{ik}\) of player \(i\) for game \(k\) is first passed through a non-linear transformation resulting in an \(F\)-dimensional vector

\[\mathbf{y}_{ik} = \text{ReLU}(\mathbf{x}_{ik}\mathbf{W} + \mathbf{b})\]

We then calculate the unnormalised attention scores

\[s_{ij} = \sum_{k} \mathbf{y}_{ik}^T \mathbf{W} \mathbf{W}_k \mathbf{y}_{jk}\]

between players \(i\) and \(j\) by first computing per-game scores using a ‘learned dot-product’ with query and key weight matrices \(\mathbf{W}\) and \(\mathbf{W}_k\) as in the original TransformerSee "The Illustrated Transformer" blog post for an intuitive explanation of the Transformer and the role of the query and weight matrices., and then summing them over the games.

The attention scores

\[\alpha_{ij} = \text{softmax}_{j}(u_{ij})\]

are obtained by taking the softmax over the unnormalised scores over the second dimension.

Finally, the \(F\)-dimension embedding

\[\mathbf{z}_{ik} = \phi\left(\sum_{v} \alpha_{ij}\mathbf{y}_{jk}\right)\]

of node \(i\) for game \(k\) is obtained by aggregating the \(\mathbf{y}_{ik}\) vectors of other nodes weighted by the attention scores, before passing the result through a 2-layer MLP \(\phi\).

The decoder outputs probabilities for each entry of the adjacency matrix by aggregating the \(k\) vectors for players \(i\) and \(j\). This is done by taking the dot product of the two vectors for each game and summing the results before feeding them into a multilayer perceptron (MLP):

\[\hat{a}_{ij} = \psi\left(\sum_{k} \mathbf{z}_{ik} \odot \mathbf{Z}_{jk}\right)\]

where \(\odot\) represents the dot product and \(\psi\) is a 2-layer MLP.

The resulting model is permutation-invariant over the set of games. This means that it produces the same predicted adjacency matrix regardless of the order in which the games are presented. To achieve this, the model computes separate node embeddings for each game and aggregates them through summation, which is a permutation-invariant operation. In practice, this property of the model ensures that we obtain consistent and reliable predictions, regardless of how the input data is ordered.

Experimental Results

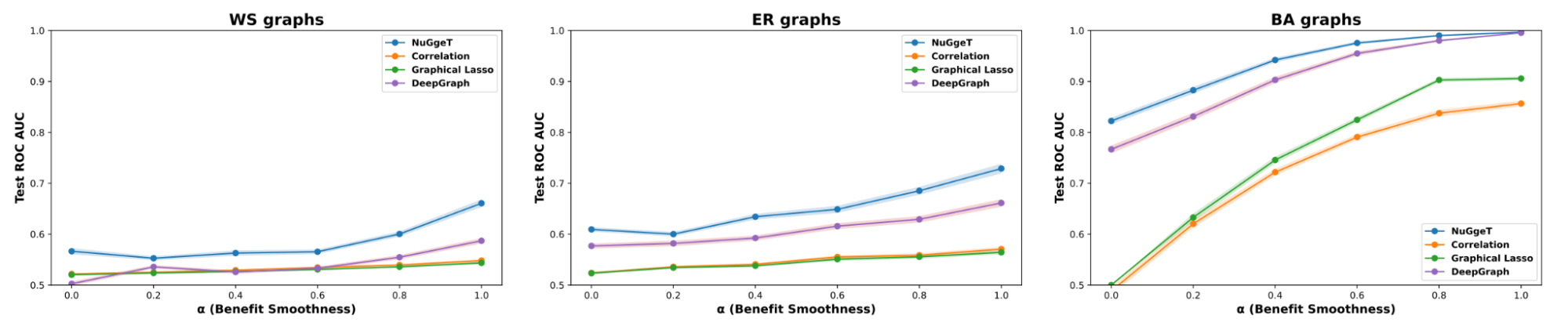
We conducted experiments to validate the effectiveness of our approach in learning the network structure from players’ actions, using both synthetic and real-world datasets. As baselines, we used DeepGraph (the only machine learning approach we are aware of), optimisation methods specific to the game type, and simple correlation and anticorrelation of actions between nodes.

On synthetic datasets, our model, NuGgeT, consistently outperformed previous methods across a range of different games and graphs types.

We report the results on Linear Influence games (see the paper for Linear Quadratic and Barik-Honorio) on three different types of synthetic graphs (Watts–Strogatz, Erdős–Rényi and Barabási–Albert) and with varying smoothness of the marginal benefit (a hyperparameter of this type of game). Our method, called NuGgeT, consistently outperforms the baselines.

The performance of our model in learning the mapping depends on the number of available games and training graphs, and we conducted ablations to evaluate both factors. Generally, a higher number of games and graphs are beneficial for our approach. However, we observe that the model performance tends to plateau at around 100 games and 500 graphs in most cases.

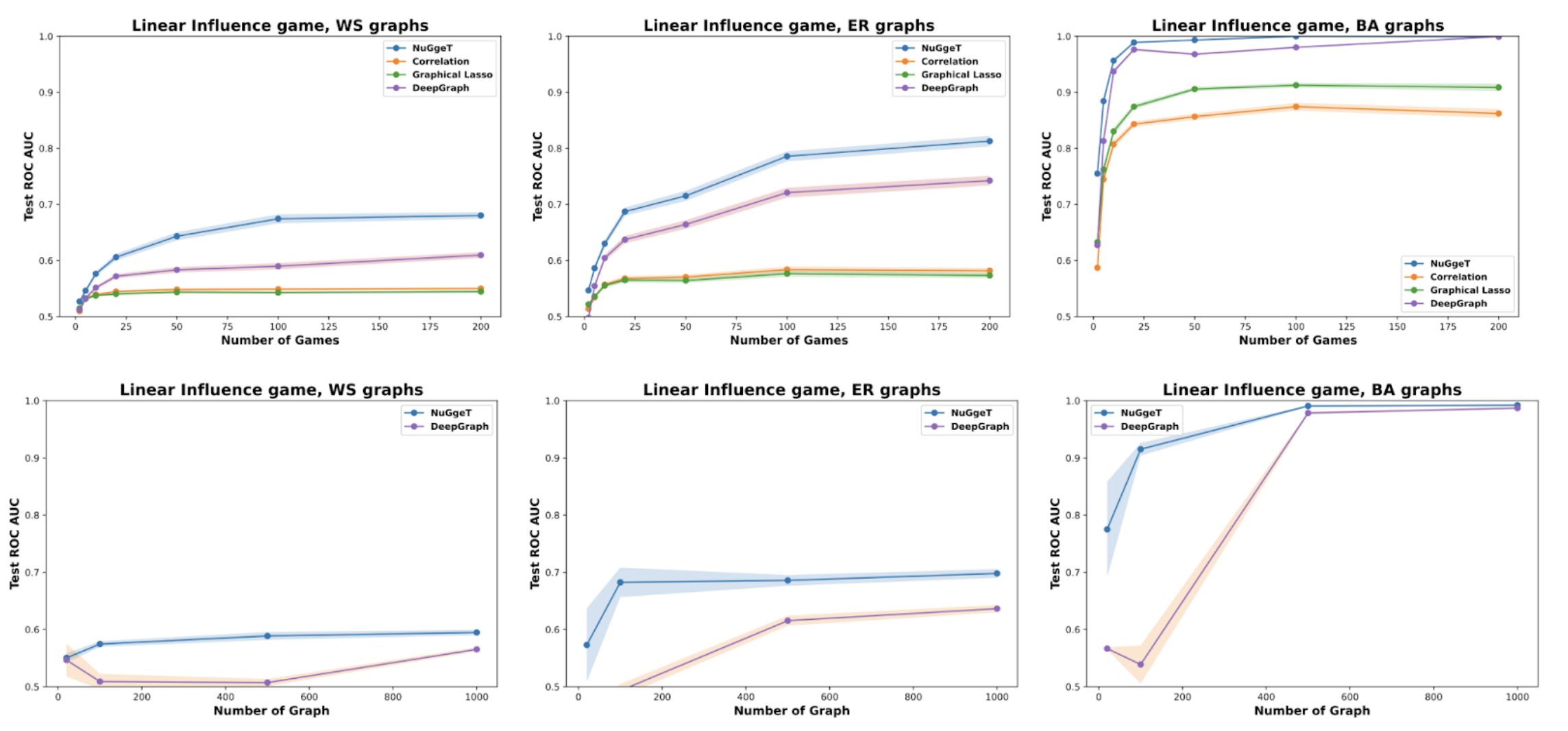
We further validated our approach on two real-world datasets: the Indian Villages datasetThe dataset accompanies the paper "The Diffusion of Microfinance" . Two authors of the paper (Abhijit Banerjee and Esther Duflo) went on to receive the 2019 Economics Nobel prize. and the Yelp Ratings datasetYelp Open dataset.. The former contains data from a survey of social networks in 75 villages in India. Each village constitutes a social network graph, where nodes are households and edges are self-reported friendships. We consider as actions the number of rooms, number of beds and other decisions families have to make related to their household. The reasoning is that if neighbours adopt a specific facility, villagers tend to gain higher payoff by doing the same, i.e., complying with social norms.

The Yelp Ratings dataset consists of user ratings of businesses and social connectivity between users. We extracted 5000 sub-graphs representing communities from the raw data, where the actions were the average rating of users for 22 categories of businesses.

On both real-world datasets, NuGgeT outperforms previous methods, showcasing the efficacy of our approach in cases where the game utility is not explicitly known. The gain is particularly large on the Indian Villages dataset, where the competing DeepGraph method fails to learn altogether. We conjecture this is due to NuGgeT being more data-efficient thanks to its built-in invariances, as confirmed by the above ablation over the number of training graphs.

The table reports ROC AUC on the test set. NuGgeT outperforms previous methods on both the two real-world datasets we tested on, confirming its efficacy in cases where the game utility function is not explicitly known.

In conclusion, our paper highlights the fruitful connection between game theory and graph machine learning, particularly in the context of network games. By developing a new machine learning approach to infer network structure from observed game outcomes, we show the potential for utilising game theory ideas to enhance machine learning and vice versa. Looking forward, there is ample opportunity to explore further connections between network games and graph neural networks, paving the way for more exciting developments in these fields.