GNNs on Directed Graphs

Graph Neural Networks (GNNs) are extremely effective at modelling relational data. However, current GNN models frequently assume the input graph to be undirected, overlooking the inherent directionality of many real-world graphs, such as social, transportation, transaction, and citation networks. In this blog post, we explore the impact of edge directionality in the context of heterophilic graphs and outline Dir-GNN, a novel message passing scheme for directed graphs allowing a separate aggregation of incoming and outgoing edges. Despite its simplicity, this scheme achieves significant performance improvement on multiple real-world heterophilic directed graphs.

Illustration based on based on Shutterstock.

This post is based on the paper Edge Directionality Improves Learning on Heterophilic Graphs, a collaboration with Bertrand Charpentier, Francesco Di Giovanni, Fabrizio Frasca and Stephan GünnemannThe title of this post, “Direction improves graph learning,” is an intentional play on a previous work J. Gasteiger, S. Weissenberger, and S. Günnemann, Diffusion improves graph learning, (2019), NeurIPS by one of the authors, which showed that a diffusion-based graph rewiring scheme (DIGL) improves the performance of GNNs in homophilic settings. Here, we focus on the heterophilic case.. The code for the paper can be found here. The same blog post has been also published on Medium.

Introduction

Many interesting real-world graphs, encountered in modelling social, transportation, financial transactions, or academic citation networks, are directed. The direction of the edges often conveys crucial insights, otherwise lost if one considers only the connectivity pattern of the graph.

In contrast, most Graph Neural Networks (GNNs) that have made remarkable strides in a variety of graph ML applications, operate under the assumption that the input graph is undirected. Making the input graph undirected has become so prevalent over the years that PyTorch-Geometric, one of the most popular GNN libraries, includes a general utility function that automatically makes graphs undirected when loading datasetsThis Pytorch-Geometric routine is used to load datasets stored in an npz format. It makes some directed datasets, such as Cora-ML and Citeseer-Full, automatically undirected without any option to get the directed version instead. .

This inclination towards undirected graphs comes, in our opinion, from two “primordial sins” of GNNs. First, undirected graphs have symmetric Laplacians with orthogonal eigenvectors offering a natural generalisation of the Fourier transform, on which early spectral GNNs relied to function properly. Second, early datasets used to benchmark GNNs were predominantly homophilic graphsHomophily refers to the assumption that nodes with similar properties (typically labels and sometimes features) tend to be connected. In homophilic graphs, the neighbourhood of a node looks like the node itself, often allowing to predict the property of a node from a simple aggregation (e.g., averaging) of the neighbours. Graphs violating this assumption are called heterophilic., such as Cora and PubmedThe Cora dataset was introduced by Andrew McCallum in the late 1990s and is for GNNs what MNIST Digits datasets is for CNNs. . On such datasets disregarding the direction by converting the directed graph into an undirected one appears to be advantageous, early evidence whereof has helped cement the “undirected” paradigm.

We challenge this status quo in our recent paper, showing that directionality can bring extensive gains in heterophilic settings.

Direction is largely useless in homophilic graphs (left), an observation that has led to the majority of current GNNs disregarding this information. In contrast, in the heterophilic setting (right), the use of direction can bring large gains (10% to 15%) if used correctly, like proposed in our Dir-GNN framework.

Measuring Homophily in Directed Graphs

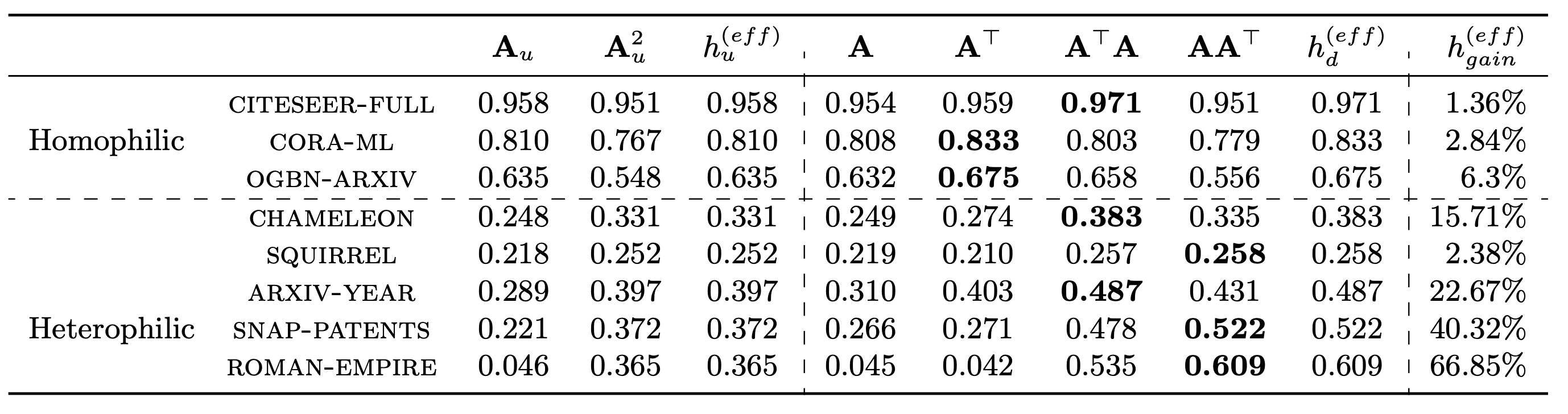
The homophily of a graph is typically measured as the fraction of neighbours with the same label as the node itself, averaged across all nodes (node homophily). For directed graphs, we propose the weighted node homophily:

\[h(\mathbf{S}) = \frac{1}{|V|} \sum_{i \in V} \frac{\sum\limits_{j \in \mathcal{N}(i)} s_{ij} I[y_i = y_j]}{\sum\limits_{j \in \mathcal{N}(i)} s_{ij}}\]

where \(I\) denotes the indicator function, \(n\) is the number of nodes, and \(\mathbf{S}\) is a general adjacency matrix, which can be picked up as \(\mathbf{A}\) or \(\mathbf{A}^\top\), or as higher-order matrices, such as \(\mathbf{AA}^\top\) or \(\mathbf{A}^2\) for directed graphs, or as the symmetric matrix \(\mathbf{A}_u = \frac{\mathbf{A} + \mathbf{A}^\top}{2}\) and its higher-order counterpart \(\mathbf{A}_u^2\), if the graph is considered as undirected.

Even when 1-hop neighbours are heterophilic, the situation may change when going to farther nodes. Compared to the undirected case, there are four distinct 2-hops in directed graphs represented by the matrices \(\mathbf{A}^2\), \((\mathbf{A}^\top)^2\), \(\mathbf{AA}^\top\) and \(\mathbf{A}^\top\mathbf{A}\), which can manifest different levels of (weighted) homophily.

Given that GNNs operate through multiple-hop aggregations, they can leverage the homophily of any 2-hop (or even further hops) of a graph. To have a comprehensive metric capturing the maximum homophily a GNN can leverage in principle, we introduce the notion of effective homophily, defined as the maximum weighted node homophily at any hop of the graph.

Empirically, we observe that the effective homophily of directed homophilic datasets is left unchanged when making the graph undirected. In heterophilic graphs, in contrast, this conversion decreases the effective homophily by almost 30% on average.

We compare the weighted homophily of both directed and undirected diffusion matrices for a variety of homophilic and heterophilic datasets. We mark in bold the highest entry for each row. The effective homophily of the directed graph ($h_d^{(\text{eff})}$) is much larger than that of the undirected graph ($h_u^{(\text{eff})}$) for heterophilic datasets, suggesting a potential gain from using directionality effectively.

A Toy Example

In particular, we observe that \(\mathbf{AA}^\top\) and \(\mathbf{A}^\top\mathbf{A}\) consistently appear to be the “most homophilic matrices” for heterophilic graphs.

To provide an intuition about why this is the case, imagine we are trying to predict the publication year of a specific academic paper, for instance, the Kipf & Welling 2016 GCN paper, given the directed citation network and the year of publication of the other papers. Consider two different kinds of 2-hop relationships: one where we look at papers cited by the papers that our paper of interest v cites (represented by the \(v^{th}\) row of the matrix \(\mathbf{A}^2\)), and another where we look at papers that cite the same sources as our paper (represented by \((\mathbf{AA}^\top)_v\)).

In the first case (\(\mathbf{A}^2\)), let us start from the GCN paper and follow its citations twice. We land on a paper by Frasconi et al. from 1998. This older paper does not give us much helpful information about when our GCN paper was published because it is too far in the past.

Simple example of a directed citation network with publication year as the node labels.

Simple example of a directed citation network with publication year as the node labels.

In the second case (\(\mathbf{AA}^\top\)), we begin with the GCN paper, follow a citation, and then come back to a paper that cites the same source, like the 2017 GAT paper. This paper is much closer to our GCN paper’s publication year and thus provides a better clue. More generally, nodes that share more references, like in our second example, will have higher scores in \(\mathbf{AA}^\top\), and thus contribute more to our final prediction.

Now, consider an undirected 2-hop relationship (\(\mathbf{A}_u^2\)), which is just the average of the four possible 2-hop matrices. This includes our first type (like Frasconi et al.), which was not very helpful. Therefore, the highly useful \(\mathbf{AA}^\top\) matrix gets diluted by less informative matrices, like \(\mathbf{A}^2\), leading to a less homophilic operator, resulting in a less reliable predictor overall.

While we have used a citation network in our example, this intuition applies more broadly. In a social network, for instance, an influencer’s characteristics are more likely to resemble those of users who share many followers with them, represented by \(\mathbf{A}^\top\mathbf{A}\). Similarly, in a transaction network, two accounts sending money to the same set of accounts (captured by \(\mathbf{AA}^\top\)), are likely to exhibit similar behaviour.

Dir-GNN: Directed Graph Neural Network

In order to leverage directionality effectively, we propose the Directed Graph Neural Network (Dir-GNN) framework, which extends MPNNs to directed graphs by performing separate aggregations over the in- and out-neighbours of a node:

\[\begin{align} \mathbf{m}^{(k)}_{i,\leftarrow} &= \mathrm{AGG}^{(k)}_{\leftarrow}\left(\{\{ \mathbf{x}_{j}^{(k-1)} : \, (j,i)\in E\}\} \right) \notag \\ \mathbf{m}^{(k)}_{i,\rightarrow} &= \mathrm{AGG}^{(k)}_{\rightarrow}\left(\{\{ \mathbf{x}_{j}^{(k-1)} : \, (i,j)\in E \}\} \right) \notag \\ \mathbf{x}_{i}^{(k)} &= \mathrm{COM}^{(k)}\left(\mathbf{x}_{i}^{(k-1)},\mathbf{m}^{(k)}_{i,\leftarrow}, \mathbf{m}^{(k)}_{i,\rightarrow}\right) \notag \end{align}\]

where the aggregation maps \(\mathrm{AGG}^{(k)}_{\leftarrow}\) and \(\mathrm{AGG}^{(k)}_{\rightarrow}\), as well as the combination maps \(\mathrm{COM}\) are learnable (usually a small neural network). Importantly, \(\mathrm{AGG}^{(k)}_{\leftarrow}\) and \(\mathrm{AGG}^{(k)}_{\rightarrow}\) can have independent set of parameters to allow for different aggregations over in- and out-edgesIt’s important to note that we are not the first to deal with directed graphs and to propose separate aggregation of in- and out-neighbours. However, our contribution is providing a more comprehensive treatment of directed graphs, which includes 1) a general framework (Dir-GNN), 2) overarching empirical evidence for the benefit of directionality, particularly in the context of heterophily, and 3) a starting point to analyse the expressiveness of models for directed graphs. See the “Related Work” section of our paper for a more thorough overview of previous works..

Interestingly, this procedural pattern resembles the one implemented by a natural extension of the 1-WL algorithm to directed graphsWhile several extensions of the WL test on directed graphs have been proposed, the variant discussed by Color Refinement and its Applications, treats in- and out-neighbours separately. . This connection is instrumental: in terms of discriminative power, we show that Dir-GNN is strictly more powerful than standard MPNNs, which either convert the graph to undirected or propagate messages only in the direction of the edges.

Our framework is also flexible: it is easy to define directed counterparts of specific architectures such as GCN, GraphSAGE or GAT. For example, we can define Dir-GCN as:

\[\mathbf{X}^{(k)} = \sigma\left(\mathbf{A}_{\rightarrow}\mathbf{X}^{(k-1)}\mathbf{W}^{(k)}_{\rightarrow} + \mathbf{A}^\top_{\rightarrow}\mathbf{X}^{(k-1)}\mathbf{W}^{(k)}_{\leftarrow}\right)\]

where \(\mathbf{A}_{\rightarrow} = \mathbf{D}_{\rightarrow}^{-1/2}\mathbf{A}\mathbf{D}_{\leftarrow}^{-1/2}\) and \(\mathbf{D}_{\leftarrow}\) and \(\mathbf{D}_{\rightarrow}\) represent the diagonal in- and out-degree matrices, respectively.

We also show that Dir-GNN, when iteratively applied over multiple layers, leads to more homophilic aggregations. Unlike other models, Dir-GNN can access the four 2-hop matrices \(\mathbf{A}^2\), \((\mathbf{A}^\top)^2\), \(\mathbf{AA}^\top\) and \(\mathbf{A}^\top\mathbf{A}\) and learn to weight them differently. In contrast, a model operating on the undirected graph has only access to \(\mathbf{A}_u^2\), while models propagating information exclusively along in- or out-edges are limited to \((\mathbf{A}^\top)^2\) and \(\mathbf{A}^2\) respectively.

Dir-GNN, thanks to its separate aggregation of the two directions, is therefore the only model operating on \(\mathbf{AA}^\top\) and \(\mathbf{A}^\top\mathbf{A}\), which we have shown to be the most homophilic matrices and therefore the most reliable predictor.

Experimental Results

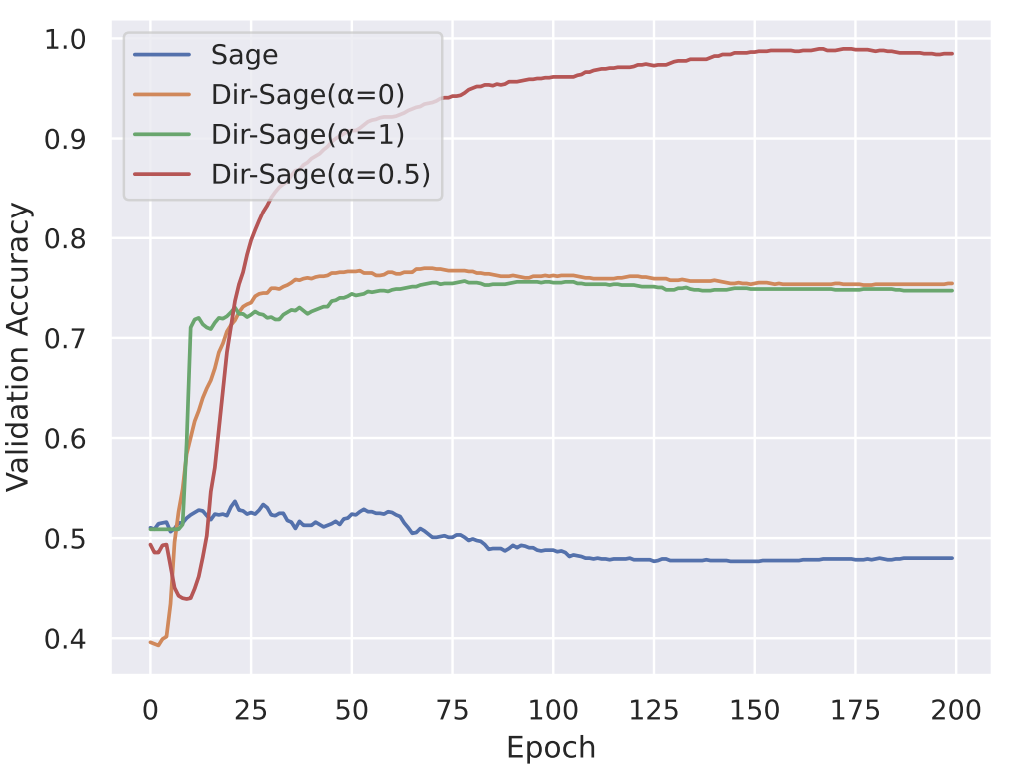
We first compared GraphSAGE and its directed extension (Dir-SAGE) on a synthetic task requiring directionality information. The results confirm that only Dir-SAGE(in+out), with access to both in- and out-edges is able to almost perfectly solve the task. The model acting on the undirected version of the graph performs no better than chance, while the models acting on only in- or out-edges perform similarly obtaining around 75% accuracy.

When examining the performance of GraphSAGE and its Dir- extensions on a synthetic task requiring directionality information, only Dir-SAGE(in+out), which utilises information from both directions, is capable of solving the task.

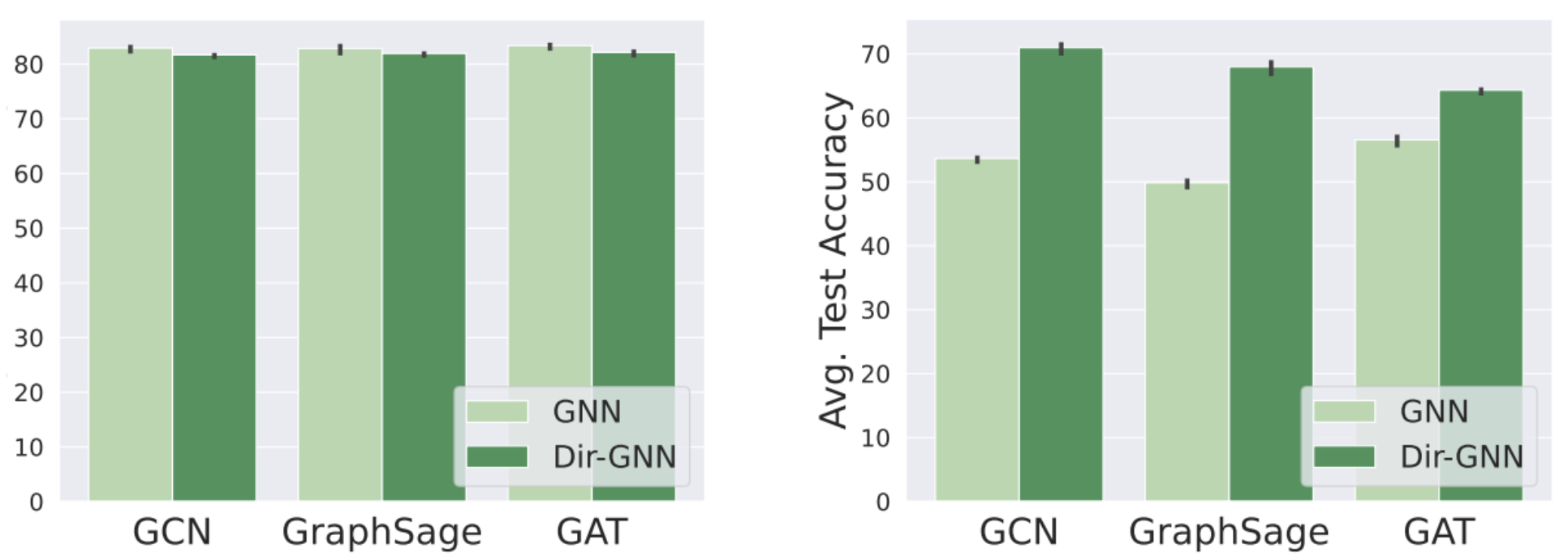
We further validated our approach with an ablation study comparing GCN, GraphSAGE and GAT base models with their Dir- extensions.On heterophilic datasets, using directionality brings exceptionally large gains (10% to 20% absolute) in accuracy across all three base GNN models. Moreover, Dir-GNN beats state-of-the-art models designed especially for heterophilic graphs. These results suggest that, when present, using the edge direction can significantly improve learning on heterophilic graphs. In contrast, discarding it is so harmful that not even complex architectures can make up for this loss of information.

New state-of-the-art results on heterophilic graphs, by using direction wisely.

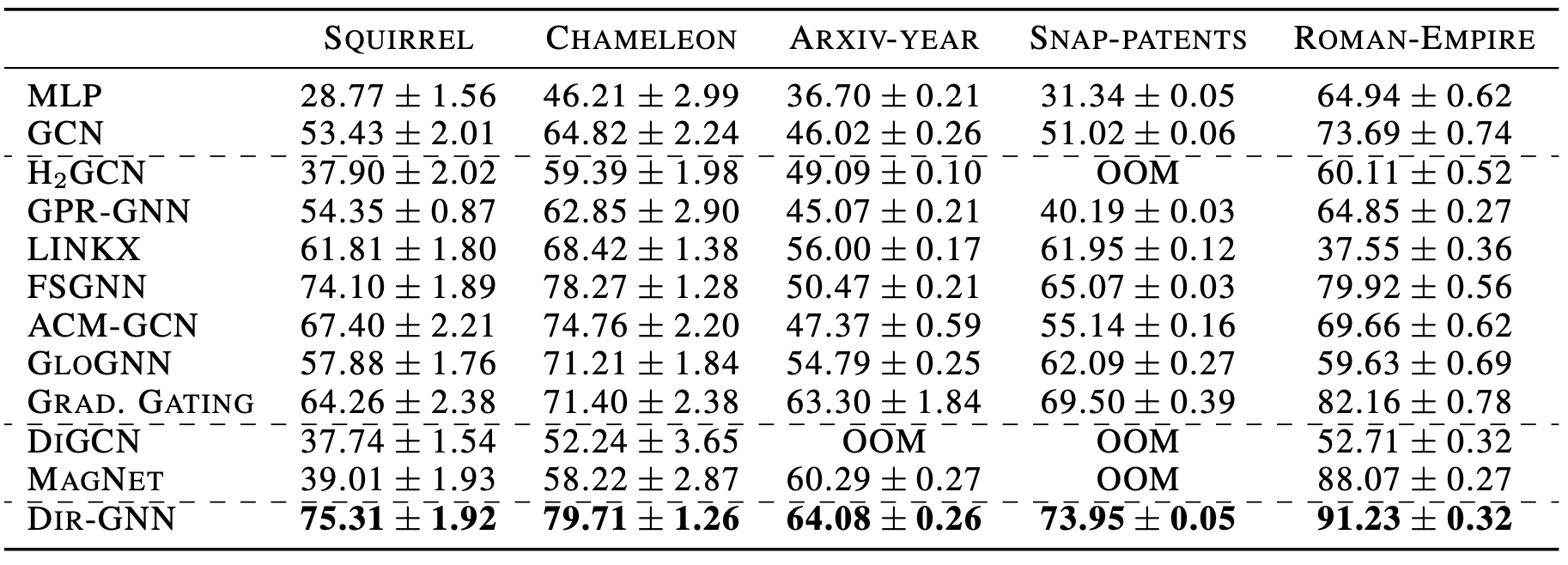
On the other hand, on homophilic datasets using directionality leaves the performance unchanged (or even slightly hurts). This is in line with our findings that using directionality as in our framework generally increases the effective homophily of heterophilic datasets, while leaving it almost unchanged for homophilic datasets.

In conclusion, our paper showcases the benefit of leveraging directionality in GNNs, particularly in the case of heterophilic graphs. We hope that these findings will instigate a paradigm shift, elevating direction as a first-class citizen in GNNs. In short, think twice before making your graph undirected!

We would like to thank Christopher Morris and Chaitanya K. Joshi for insightful discussions and pointing us to relevant papers.